La sección Áurea y la divina proporción

La proporción áurea fue usada como una de las primeras reglas de composición fotográfica. Anteriormente lo había sido también en la pintura y la expresión artística en general.

La proporción áurea es uno de los principios formales de la composición visual que ha sido utilizado desde la antigüedad. Esta proporción se ha encontrado tanto en murales egipcios como mesopotámicos y aztecas, entre otras muchas culturas.

A lo largo de la historia los artistas y científicos han tratado de analizar qué hace bueno y efectivo un diseño o una composición fotográfica.

Matemáticos griegos, entre los siglos III y V antes de Cristo, teorizaron sobre lo que llamaron la Proporción Áurea. Esta proporción es el número irracional que vincula dos segmentos de la misma recta.

Los griegos identificaron una regla que parecía ser una proporción mágica o divina. Esta divina proporción divide el espacio o las líneas en una imagen placentera. Sus estudios los llevaron finalmente a describir las dimensiones matemáticas precisas de esta proporción ideal y le llamaron número áureo o número de oro.

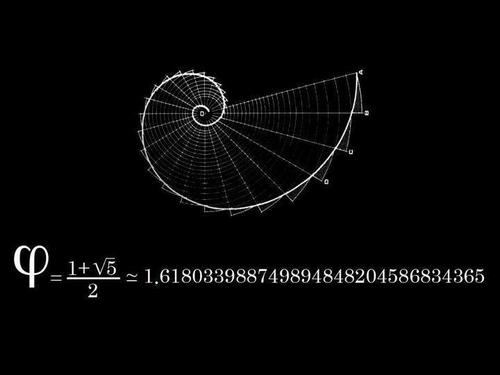
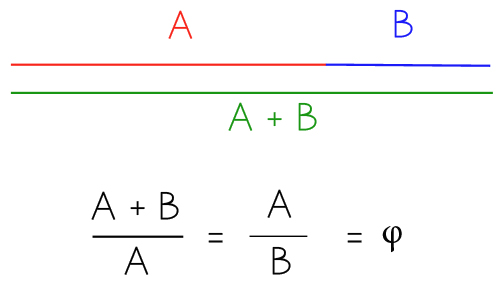
Este número áureo, también llamado Número Phi se halló dividiendo un segmento en dos partes, A y B. La parte A es más larga que la parte B y la longitud total de la recta tiene la misma relación con A que A con B. En términos algebraicos se expresa con la siguiente ecuación: (A + B)/A = A/B. Si, por ejemplo, A, tiene un valor de 1, B dará como resultado el número phi, que tiene un valor de 1,618.

La sucesión de Fibonacci

Fibonacci es el padre de la sucesión de números que lleva su nombre y que está íntimamente relacionada con la proporción áurea. La sucesión de Fibonacci es una serie de números infinitos en el que cada una de esas cifras es el resultado de la suma de las dos anteriores. La sucesión es la siguiente, 0, 1, 1, 2, 3, 5, 8, 13, etc., donde vemos que 0+1 = 1, 1+1= 2, 2+1= 3, 2+3= 5 y así sucesivamente.

Curiosamente, el resultado de la división de cada pareja de números consecutivos de su sucesión, da como resultado un número muy cercano al número Phi.

A partir de este hallazgo se empezaron a hacer representaciones gráficas de la sucesión de Fibonacci. Este rectángulo, por ejemplo, está dividido en partes más pequeñas siguiendo la sucesión y con medidas que, al dividirlas, da como resultado el número áureo.

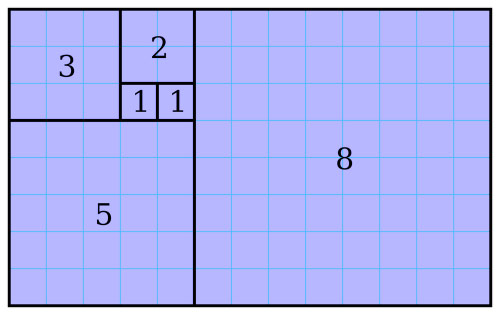
Si a esta serie de rectángulos se le traza una línea en forma de espiral uniendo algunos de los vértices hallamos la tan famosa Espiral de Oro. Esta espiral se da con muchísima frecuencia en la naturaleza. La podemos ver en determinadas plantas, en flores e incluso en conchas de caracoles.

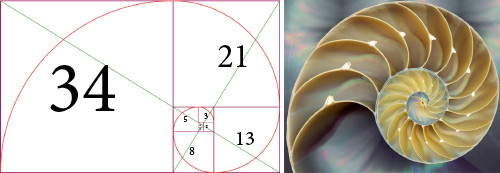
En fotografía se ha utilizado esta proporción áurea desde los orígenes de la disciplina, intentando encuadrar los objetos en los puntos fuertes de esta espiral. Los resultados suelen ser armónicos y equilibrados utilizando esta técnica de composición.

A pesar de todo, estas leyes no son para seguirlas al pie de la letra. Solo son normas que nos pueden ser muy útiles para comenzar a componer partiendo de ellas y que podemos emplearlas o no según nuestro criterio y su adecuación al tema que se esté trabajando.

◄ Anterior		Siguiente ►
Reglas fundamentales para componer una fotografía		Regla de los 3 tercios